Linearly Solvable Mean-Field Traffic Routing Games

In this project, we study the strategic behavior of drivers travelling over an urban traffic network in the limit of many drivers. We propose an incentive mechanism (toll charge) which is congestion-dependent and affine in the logarithm of the number of drivers taking the same route. We apply the mean-field game (MFG) theory to this problem and show that the backward Hamilton-Jacobi-Bellman and forward Fokker-Planck-Kolmogorov equations can be solved independently. We show a mean-field equilibrium (MEF) is obtained through a linearly-solvable set of equations, and the MFE is strongly time-consistent. We extend the results for multi-team settings.

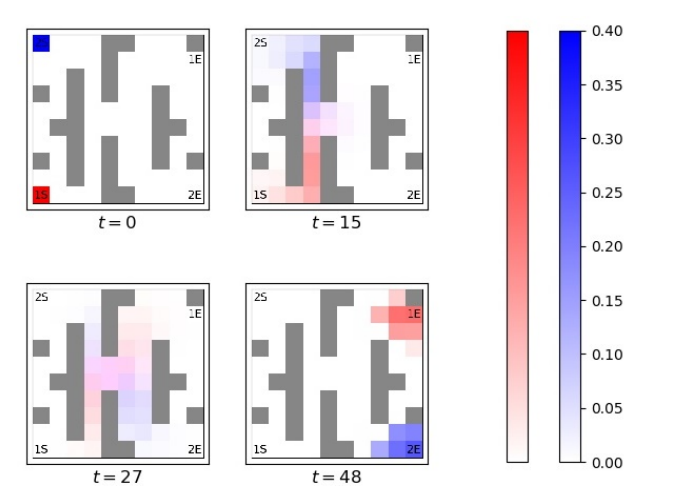
Optimal density propagation of team one (red) and team two (blue) in a sample environment.

Related Publications:
Linearly Solvable Mean-Field Traffic Routing Games, T. Tanaka, E. Nekouei, AR. Pedram, KH. Johansson, IEEE Transactions on Automatic Control, 2020 [Link]
Linearly-Solvable Mean-Field Approximation for Multi-Team Road Traffic Games, AR. Pedram, T. Tanaka, IEEE Conference on Decision and Control, 2019 [Link]