Rationally Inattentive Vision and Planning
This research is motivated by the increasing need for simultaneous perception and action planning in modern information-rich autonomy. Due to the wide availability of low-cost and high-performance sensing devices, obtaining a large amount of sensor data has become easier in many applications. Nevertheless, operating a sensor at its full capacity may not be the best strategy for resource-constrained robots, especially if it drains its scarce power or computational resources with little benefit. As sensor modalities increase, how to achieve a given task with minimum perceptual resources, e.g., with reduced sensing/communication frequencies or sensor gains, becomes increasingly relevant.
In the first phase of this project, we propose a task-dependent attention allocation for vision-based autonomous navigation inspired from attention mechanisms in humans. The proposed mechanism helps the robot to analyze the visual information relevant to the task at hand while neglecting the rest of the available data. In the second phase, we develop a framework to predict and incorporate the perception cost in the motion planning stage, which help the autonomous agent to find motion plans that can be executed with both minimum control and perception efforts. We modify existing motion-planning algorithms (like sampling-based methods) to be able to integrate the perception effort.
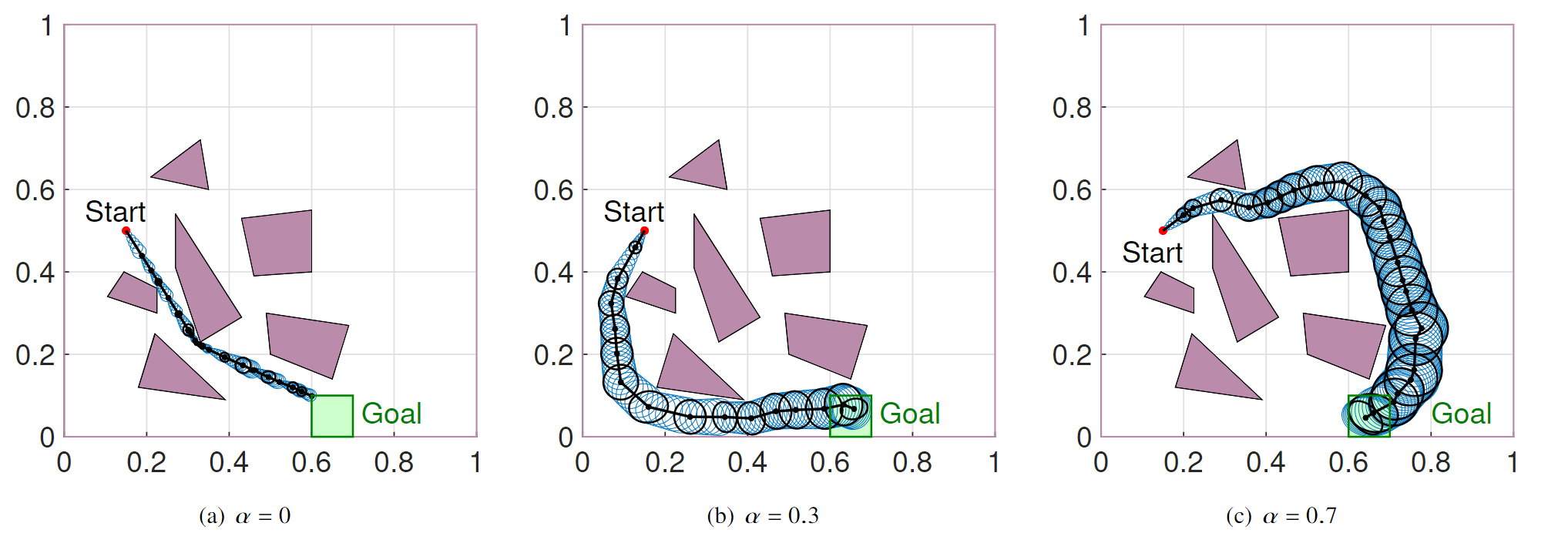
Optimal path plans obtained for different values of perception effort intensity α.
Related Publications:
A Smoothing Algorithm for Minimum Sensing Path Plans in Gaussian Belief Space AR. Pedram , T. Tanaka, American Control Conference, 2023 [Link]
Gaussian Belief Space Path Planning for Minimum Sensing Navigation, AR. Pedram , R. Funada, T. Tanaka, IEEE Transactions on Robotics, 2022 [Link]
Dynamic Allocation of Visual Attention for Vision-based Autonomous Navigation under Data Rate Constraints, AR. Pedram, R. Funada, T. Tanaka, IEEE Conference on Decision and Control, 2021 [Link]
Rationally Inattentive Path-Planning via RRT*, AR. Pedram, J. Stefan, R. Funada, T. Tanaka, American Control Conference, 2021 [Link]
Feedback Capacity of Gaussian Channels with Memory: Implications in Autonomy
In this research, we study the information-theoretic problem of computing the capacity of Gaussian channels with partial feedback whose dynamics are expressed as a linear state-space system, where we seek the maximum number of bits that could be communicated reliably with bounded input power. We show this problem appears in different contexts of autonomy, like in the identification of linear dynamic systems and in the privacy of linear dynamic systems in the cloud-based control setting. In this project, I establish several theoretical results. For instance, I show the identification rate of linear dynamic systems is fundamentally upper bounded by a linear function of the identification step, and no policy can achieve a super-linear convergence rate. I illustrate the privacy of dynamical systems in cloud-based settings is not necessarily a monotone function of the noise levels of privacy masks. I also show both input and out masks are required, as opposed to static date-base setting.
Related Publications:
Optimized Data Rate Allocation for Dynamic Sensor Fusion over Resource Constrained Communication Networks, H. Jung, AR. Pedram, T. Cuvelier, T. Tanaka, International Journal of Robust and Nonlinear Control, 2023 [Link]
Online Parameter Identification of Linear Dynamical Systems through the Lens of Feedback Channel Coding Theory, AR. Pedram, T. Tanaka, American Control Conference, 2020 [Link]
Bidirectional Information Flow and the Roles of Privacy Masks in Cloud-Based Control , AR. Pedram, T. Tanaka, M. Hale, IEEE Information Theory Workshop, 2019 [Link]
Some Results on the Computation of Feedback Capacity of Gaussian Channels with Memory, AR. Pedram, T. Tanaka, Allerton Conference on Communication, Control,
and Computing, 2018 [Link]
Linearly Solvable Mean-Field Traffic Routing Games
In this project, we study the strategic behavior of drivers travelling over an urban traffic network in the limit of many drivers. We propose an incentive mechanism (toll charge) which is congestion-dependent and affine in the logarithm of the number of drivers taking the same route. We apply the mean-field game (MFG) theory to this problem and show that the backward Hamilton-Jacobi-Bellman and forward Fokker-Planck-Kolmogorov equations can be solved independently. We show a mean-field equilibrium (MEF) is obtained through a linearly-solvable set of equations, and the MFE is strongly time-consistent. We extend the results for multi-team settings.
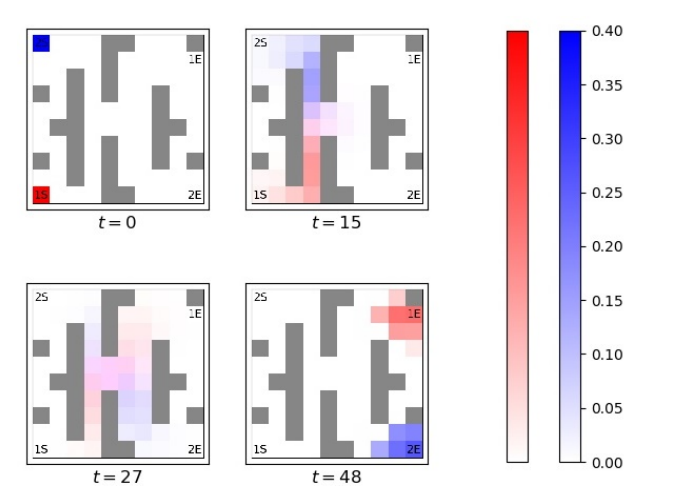
Optimal density propagation of team one (red) and team two (blue) in a sample environment.
Related Publications:
Linearly Solvable Mean-Field Traffic Routing Games, T. Tanaka, E. Nekouei, AR. Pedram, KH. Johansson, IEEE Transactions on Automatic Control, 2020 [Link]
Linearly-Solvable Mean-Field Approximation for Multi-Team Road Traffic Games, AR. Pedram, T. Tanaka, IEEE Conference on Decision and Control, 2019 [Link]